1538. Мысли наоборот
Деление
плоскости на части различными фигурами - известная задача в области
компьютерных наук. Внизу на рисунке изображено несколько таких диаграмм. На
рисунке 1 четыре окружности могут разделить плоскость максимум на 14 областей,
четыре эллипса могут разделить плоскость максимум на 26 областей, а три
треугольника - на 20 частей. Классическая задача состоит в том, чтобы найти
максимальное количество областей, на которое могут разделить плоскость m фигур. Например, для окружностей известна
формула m2 – m + 2. В смешанном случае (когда
пересекается несколько типов фигур) максимально возможное количество областей
найти также не трудно.
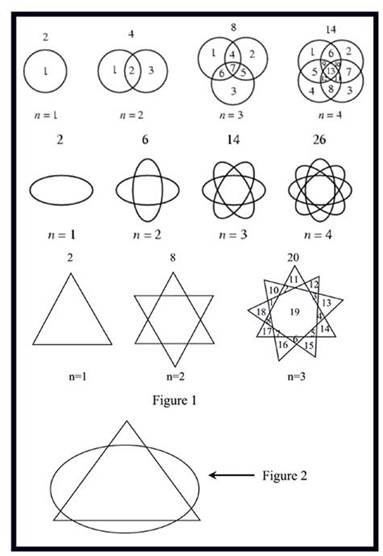
На рисунке 2 восемь областей
образованы пересечением одного эллипса и одного треугольника. Здесь Вам следует
решить обратную задачу. По заданному максимальному количеству областей следует
найти количество эллипсов, окружностей и треугольников, которое могло их
образовать.
Вход. Состоит из менее
чем 300 строк. Каждая строка содержит 32-битовое беззнаковое целое N –
максимальное количество областей, образованное m эллипсами, n
окружностями и p треугольниками.
Последняя строка содержит -1 и не обрабатывается. Все числа кроме -1 в
последней строке положительны.
Выход. Для каждого
теста необходимо вывести две или более строк. Первая строка каждого теста
содержит его номер. Каждая из следующих строк содержит три целых числа –
возможные значения m, n и p,
для которых образуется максимальное количество областей N. Если существует
несколько решений, то их следует отсортировать сначала по возрастанию m, а потом по возрастанию n. Если решения не существует, то
вывести строку “Impossible.”. Выводить следует только те решения, для которых 0
≤ m < 100, 0 ≤ n < 20000 и 0 ≤ p < 100.
|
Пример
входа |
Пример
выхода |
20 10 -1 |
Case 1: 0 0 3 0 1 2 1 0 2 1 3 0 Case 2: Impossible. |
РЕШЕНИЕ
комбинаторика
+ перебор
Анализ алгоритма
Пусть n
фигур разбивают плоскость на f(n) частей. Одна фигура разбивает
плоскость на 2 части. Каждая следующая n - ая фигура должна иметь
максимально возможное количество пересечений k с каждой из (n –
1) предыдущих фигур. Две окружности могут пересекаться максимум в двух точках (k
= 2), два эллипса в четырех (k = 4), а два треугольника в шести (k
= 6). Тогда
f(n) = f(n
– 1) + k * (n – 1),
f(1) = 2
Решим
рекуррентное уравнение:
f(n) = k
* ((n – 1) + (n – 2) + … + 1) + 2 == k * ![]() + 2
+ 2
Заметим, что
f(0) = 1 для любого k (ноль фигур делят плоскость на одну часть).
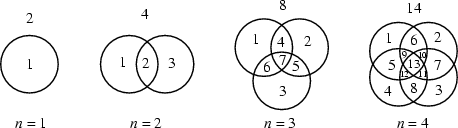
Окружности
на плоскости
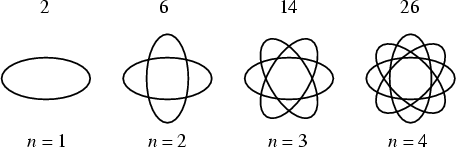
Эллипсы на плоскости
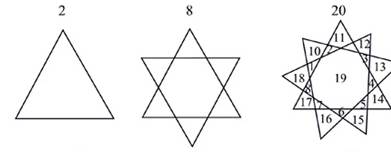
n = 1 n
= 2 n = 3
Треугольники на плоскости
Из выше
приведенной формулы следует, что m эллипсов, n окружностей и p
треугольников могут разделить плоскость максимум на 2 + 2m (m –
1) + n (n – 1) + 4mn + 3p (p – 1) + 6pn
+ 6pm частей. m эллипсов и n окружностей могут иметь
максимум 4mn точек пересечения, p треугольников и n
окружностей или m эллипсов – соответственно 6pn и 6pm
точек пересечения. Приравняем это значение к N и перепишем выражение как квадратное уравнение относительно n:
n2 + n (4m
+ 6p – 1) + 2 + 2m (m – 1) + 3p (p – 1) + 6pm
– N = 0
Если
дискриминант уравнения является полным квадратом для некоторых целых m и
p, 0 £ m, p < 100, то ищем соответственное
неотрицательное значение n и проверяем его принадлежность интервалу 0 £ n < 20000. Остается перебрать все пары (m, p)
из заданного интервала и для каждой из них решить квадратное уравнение.
Найденные тройки остается упорядочить по заданному в условии задачи правилу.
Исключительными
являются следующие случаи:
·
если N = 1, то ответом является единственная тройка (0, 0,
0);
·
если N равно нулю или нечетно (кроме N = 1), то искомых троек не существует.
Пример
Рассмотрим
первый тест. На 20 частей плоскость можно разбить следующими комбинациями
фигур: 3 треугольника, 1 окружность и два треугольника, 1 эллипс и два
треугольника, 1 эллипс и две окружности.
Реализация алгоритма
Читаем входные данные и выводим номер теста CaseNo.
CaseNo = 1;
while(scanf("%lld",&N),
N != -1)
{
printf("Case
%lld:\n",CaseNo++);
Если входное
значение N равно 1, то ответом
будут три нуля.
if (N == 1)
{
printf("0 0
0\n"); continue;
}
Если N равно
нулю или нечетно, то искомых троек не существует.
if ((N == 0)
|| (N % 2))
{
printf("Impossible.\n");continue;
}
Введем
переменную флаг found, который будет
равен 1, если для заданного N будет найдена хотя бы одна тройка - решение.
Изначально присвоим found значение 0.
found = 0;
Совершаем
перебор всех возможных значений m, p (0 £ m, p < 100). По ходу вычисляем максимальное
количество частей, на которое фигуры делят плоскость. Если на каком-то этапе
значение суммы (res или res1) станет большей N, то выходим из
цикла (нет смысла перебирать последующие значения соответствующей переменной).
Чтобы не
собирать все искомые тройки в некоторой структуре данных с последующей их
сортировкой, организуем перебор так, чтобы сразу после нахождения тройки -
решения выводить ее на печать. Для этого организуем перебор эллипсов от 0 до 99
(по возрастанию m), а перебор
треугольников совершим по убыванию. Заметим, что для каждой перебираемой пары (m, p)
у нас будет не более одного подходящего значения n (так как нас интересуют только неотрицательные значения n), а p и n зависят друг от друга
в обратной пропорциональности. То есть перебирая значения p по убыванию, мы будем получать тройки - решения по возрастанию n.
for(m = 0; m < 100; m++) // m =
Ellipses
{
Значение переменной res равно максимальному количеству
частей, на которое могут разбить плоскость m
эллипсов. res1 содержит максимальное
количество частей, на которое могут разбить плоскость m эллипсов и p
треугольников.
res = 2 + 2 * m * (m - 1);
if (res
> N) break;
for(p = 99;
p >= 0; p--) // p = Triangles
{
res1 = res + 3 * p * (p - 1) + 6 * m * p;
if (res1
> N) continue;
Имеются значения
m и p. Решаем квадратное уравнение
n2 + n (4m
+ 6p – 1) + 2 + 2m (m – 1) + 3p (p – 1) + 6pm
– N = 0
относительно n.
Вычисляем дискриминант det уравнения x2 + bx + res1 – N = 0. Если он
неотрицательный, является полным квадратом, а положительный корень квадратного
уравнения целый, то находим n и проверяем его принадлежность интервалу 0
£ n < 20000. Если все условия выполнены, то
выводим тройку (m, n, p).
b = 4 * m + 6 * p - 1;
det2 = b * b - 4 * (res1 - N);
if (det2
>= 0)
{
det = (long
long)sqrt(1.0 * det2);
if
((det * det == det2) && ((-b + det) % 2 == 0))
{
n = (-b + det) / 2; // n = Circles
if
((n >= 0) && (n < 20000))
{
printf("%lld
%lld %lld\n",m,n,p);
found = 1;
}
}
}
}
}
Если решения не
найдены, то выводим соответствующее сообщение.
if (!found) printf("Impossible.\n");
}
Java реализация
import java.util.*;
public class Main
{
//Find the solutions x^2 + B*x + C = 0 in integers
static long Solve(long B, long C)
{
long D = B * B - 4 * C;
if (D >= 0)
{
long R = (long)(Math.pow(D,0.5) + 0.5);
if ( (D == R * R) && ((- B + R) % 2 == 0) )
return (- B + R) /
2;
}
return -1;
}
public static void FindSolution(long N)
{
if(N == 1)
{
System.out.println("0 0 0");
return;
}
if((N == 0) || (N % 2 == 1))
{
System.out.println("Impossible.");
return;
}
boolean Flag = true;
for(int mEllipses = 0; mEllipses < 100; mEllipses++)
{
long C1 = 2 + 2 * mEllipses * (mEllipses - 1);
if (C1 > N) break;
for(int pTriangles = 99; pTriangles >= 0; pTriangles--)
{
// n^2 + n (4m + 6p - 1) + 2 + 2m (m - 1) + 3p (p - 1) +
6pm - s = 0
long B = 4 * mEllipses + 6 * pTriangles - 1;
long C = C1 + 3
* pTriangles * (pTriangles - 1) +
6 * mEllipses * pTriangles;
if (C > N) continue;
C -= N;
long nCircles = Solve(B,C);
if ( (nCircles >= 0) && (nCircles < 20000) )
{
System.out.println(mEllipses + " " + nCircles + " " +
pTriangles);
Flag = false;
}
}
}
if(Flag) System.out.println("Impossible.");
}
public static void main(String[] args)
{
Scanner in = new Scanner(System.in);
long N = in.nextLong();
int CaseNo = 0;
while(N >= 0)
{
CaseNo++;
System.out.println("Case " + CaseNo + ":");
FindSolution(N);
N = in.nextLong();
}
}
}